
배음 (Harmonics) : 하모닉스
일정한 주파수를 가지는 사인파(음향에서 순음,pure Tone이라고도 부른다) 를 스피커에 출력 시켜 보면 스피커가 일정하게 앞/뒤로 진동하면서 그 소리를 만드는 것을 볼 수 있어요. 그러나 사인파 이외의 소리를 입력하면 스피커의 움직임이 아주 불규칙하다는 것도 알 수 있어요. 또 들리는 소리도 일정한 사인파의 소리와는 아주 다른 소리가 나와요. 이것은 음향에서 각기 다른 소리가 가지는 음색(Tone)이라고 말하는 부분이에요.
같은 음높이, 다시 말해 동일한 진동수를 가지는 소리도 서로 다른 음색을 가질 수 있어요. 이는 각각 서로 다른 음색을 가지고 있기 때문이죠. 예를 들어, 같은 440Hz의 A라는 음정으로 연주된 피아노의 소리와 기타의 소리가 전혀 다른 것은 이제 설명될 순음 이외의 모든 소리가 가지고 있는 복합적인 음색의 구조 때문이에요. 이 복합적인 음색의 구조에서 가장 큰 역할을 하는 것이 배음(Harmonics)이에요.
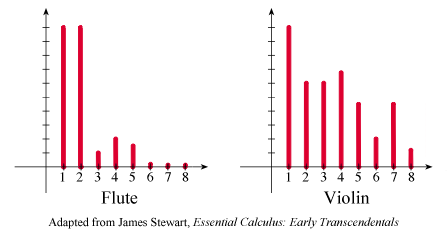
배음은 소리의 특성을 나타내는 중요한 역할을 해요. 모든 소리는 기본 음높이를 규정짓는 주파수(진동수)와 그 주파수의 정수배(2배,3배,4배,,등의) 주파수의 소리가 합쳐진 복합음의 형태를 가지고 있어요. 어떤 악기가 440Hz의 A4음으로 연주된다고 할 때 이 소리는 440Hz의 소리와 2배인 880Hz, 그리고 3배인 1,320Hz 4배인 1,760Hz.. 등등 의 소리가 함께 나옵니다. 이와 같은 법칙의 복합음을 모든 소리가 가지지만 서로 다른 음색을 내는 이유는 이 정수배로 나타나는 여러 가지 다른 주파수를 가지는 소리의 양과 숫자, 그리고 위치에 따라서 다른 소리가 만들어지기 때문이에요. 위그림에서 보는 것과 같이 같은 음을 연주하는 플룻과 바이올린도 서로 다른 배음을 가지고 있어요.


배음은 어떤 주파수의 소리에 대해 그 주파수의 정수배인 주파수가 혼합되어 있는 현상입니다. 예를 들어 440Hz의 A라는 음정은 880Hz, 1320Hz, 1760Hz 등의 배음을 가지고 있습니다. 이렇게 배음이 혼합되어 있어서 같은 음높이를 가지더라도 서로 다른 악기들이 다른 음색을 내게 됩니다.
다음은 배음 현상을 예시로 들어본 세 가지 악기입니다.
- 플룻: 플룻은 440Hz의 A라는 음정을 연주할 때, 이 음정과 880, 1320, 1760, 2200, 2640Hz 등의 배음을 가지고 있습니다. 이러한 배음들이 혼합되어 플룻만의 특별한 음색을 만들어냅니다.
- 바이올린: 바이올린은 440Hz의 A라는 음정을 연주할 때, 이 음정과 880, 1320, 1760, 2200, 2640, 3080, 3520, 3960Hz 등의 배음을 가지고 있습니다. 플룻과는 다르게 바이올린은 더 많은 배음을 가지고 있어서 더욱 풍부한 음색을 만들어냅니다.
- 트럼본: 트럼본은 440Hz의 A라는 음정을 연주할 때, 이 음정과 880, 1320, 1760, 2200, 2640, 3080, 3520, 3960, 4400, 4840Hz 등의 배음을 가지고 있습니다. 바이올린보다는 배음이 적지만, 낮은 음역을 담당하는 악기이기 때문에 더욱 깊고 다채로운 음색을 만들어냅니다.

악기로 비유하자면 배음은 색소폰을 연주하는 것과도 비슷해요. 색소폰은 하나의 음만으로는 소리를 구성하기 어려워서 여러 개의 음을 섞어서 음색을 만들어냅니다. 이와 마찬가지로 배음도 여러 주파수를 섞어서 다양한 음색을 만들어냅니다.

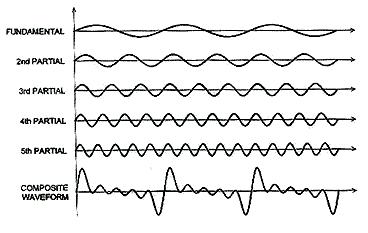
위의 그림을 보세요! 1, 1/2, 1/3, 1/4 1/5 주기의 파형이 순서대로 그려져 있습니다. 이들 파형을 합치면, 마지막으로 그려진 복합 파형이 만들어집니다. 파형 덧셈을 배우려면, 수학적인 공식을 이용해서 계산하고 그래프를 그리는 방법을 사용해야 합니다. 그러나 실제 음향에서는 반대의 상황이 적용됩니다. FFT Analyzer와 같은 기기를 사용하면, 입력된 파형을 주파수별로 분석해 줄 수 있습니다. 각 주파수에 해당하는 파형을 그려보면(같은 시간을 기준으로), 왼쪽 그림과 같은 각각의 파형을 볼 수 있습니다. 가장 위에 그려진 파형은 440Hz의 A4음이라고 생각해 볼 수 있습니다. (물론 그림의 한 주기는 1/440초로 자른 시간 간격이겠지만) 각각 880Hz, 1320Hz, 1760Hz, 2200Hz의 파형입니다. 마지막 그래프는 기본 440Hz의 주파수에 각 파형들의 진폭만큼의 배음을 가지는 소리 모양입니다.
이 배음은 음색 조정과 같은 부분에서 아주 중요한 역할을 합니다. 소리를 듣고 그 소리가 플룻 소리인지, 개 짖는 소리인지 알 수 있는 것은 바로 이 배음이 다른 각각의 소리를 이미 기억하고 있는 사람의 뇌가 구분해 내기 때문입니다. 오버톤(Overtone)은 기본 주파수(Fundammanta Frequency)를 제외하고, 정수배수인 배음을 포함한 발생한 모든 음을 말합니다.
배음(Harmonics) 주파수
| 기본 주파수(Fundamental Frequency) | 440Hz |
| 1차 배음 | 880Hz |
| 2차 배음 | 1320Hz |
| 3차 배음 | 1760Hz |
| 4차 배음 | 2200Hz |
위의 표는 440Hz의 A4음이 기본 주파수(Fundamental Frequency)로 설정되어 있고, 1차 배음부터 4차 배음까지의 주파수를 보여줍니다. 배음(Harmonics)은 기본 주파수(Fundamental Frequency)를 제외하고, 정수배수인 주파수가 혼합된 현상입니다. 이것은 각각의 악기가 서로 다른 음색을 낼 수 있는 이유 중 하나입니다
참고서적 - 장호준의 음향시스템 핸드북
책 (장호준 : 음향시스템 핸드북) : 구매링크
음향시스템 핸드북 : 네이버 도서
네이버 도서 상세정보를 제공합니다.
search.shopping.naver.com
'음향(Sound) > 음향 이야기' 카테고리의 다른 글
| 음향이론8.귀 (Ear) (0) | 2023.03.25 |
|---|---|
| 음향이론7.소리의 성질 (nature of sound) 굴절/회절/반사/흡음률/확산 (0) | 2023.03.24 |
| 음향이론5.주파수 응답 (Frequency response) (0) | 2023.03.17 |
| 음향이론4.동적 범위 (다이내믹 레인지) 와 헤드룸 /피크레벨 과 노이즈 플로어 (0) | 2023.03.13 |
| 음향이론3.위상(phase) . 위상 차(Phase Difference) 에대해서 / 위상 간섭 / 위상 동조 (0) | 2023.03.13 |



